Is It Possible to Write the Sum of Natural Numbers as a Continuous Funtion
Given a number n, the task is to check whether it can be expressed as a sum of two or more consecutive numbers or not.
Examples:
Input : n = 10 Output : true It can be expressed as sum of two consecutive numbers 1 + 2 + 3 + 4. Input : n = 16 Output : false It cannot be expressed as sum of two consecutive numbers. Input : n = 5 Output : true 2 + 3 = 5
There is a direct and quick method to solve this. If a number is a power of two, then it cannot be expressed as a sum of consecutive numbers otherwise Yes.
The idea is based on below two facts.
1) Sum of any two consecutive numbers is odd as one of them has to be even and the other odd.
2) 2n = 2n-1 + 2n-1
If we take a closer look at 1) and 2), we can get the intuition behind the fact.
Below is the implementation of the above idea.
C++
#include<bits/stdc++.h>
using namespace std;
bool canBeSumofConsec(unsigned int n)
{
return ((n&(n-1)) && n);
}
int main()
{
unsigned int n = 15;
canBeSumofConsec(n)? cout << "true" :
cout << "false" ;
return 0;
}
Java
class Test
{
static boolean canBeSumofConsec( int n)
{
return (((n&(n- 1 ))!= 0 ) && n!= 0 );
}
public static void main(String[] args)
{
int n = 15 ;
System.out.println(canBeSumofConsec(n) ? "true" : "false" );
}
}
Python3
def canBeSumofConsec(n) :
return ((n&(n - 1 )) and n)
n = 15
if (canBeSumofConsec(n)) :
print ( "true" )
else :
print ( "false" )
C#
using System;
class Test
{
static bool canBeSumofConsec( int n)
{
return (((n & (n - 1)) != 0) && n != 0);
}
public static void Main()
{
int n = 15;
Console.Write(canBeSumofConsec(n) ? "True" : "False" );
}
}
PHP
<?php
function canBeSumofConsec( $n )
{
return (( $n & ( $n - 1)) && $n );
}
$n = 15;
if (canBeSumofConsec( $n ))
echo "true" ;
else
echo "false" ;
?>
Javascript
<script>
function canBeSumofConsec(n)
{
return (((n&(n-1))!=0) && n!=0);
}
let n = 15;
document.write(canBeSumofConsec(n) ? "true" : "false" );
</script>
Output:
True
Time Complexity: O(1)
Auxiliary Space: O(1)
Another Approach :
Let number chosen to represent N as a sum of consecutive numbers be X + 1, X + 2, X + 3 …. Y
Sum of these chosen numbers = Sum of first Y natural numbers – Sum of first X natural number
Sum of first Y natural number =
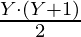
Sum of first X natural number =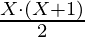
We know that,
N = Sum of first Y natural number – Sum of first X natural number
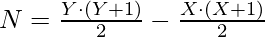

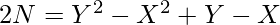
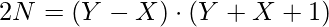
Let Y – X = a, Y + X + 1 = b
Y + X + 1 > Y – X, b > a
,
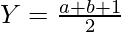
2N = a * b
It means that a and b are factor of 2N , we know that X and Y are integers so,
1. b – a – 1 => multiple of 2 (Even number)
2. b + a + 1 => multiple of 2 (Even number)
Both conditions must be satisfied
From 1 and 2 we can say that either one of them (a, b) should be Odd and another one Even
So if the number (2N) has only odd factors (can't be possible as it is an even number (2N not N) ) or only even factors we can't represent it as a sum of any consecutive natural numbers
So now, we have to now only check whether it has an odd factor or not
1. If the number (2N not N) does not have any odd factor (contains only even factor means can be represented as ![]() ) then we can't represent it as a sum of consecutive number
) then we can't represent it as a sum of consecutive number
2. If the number (2N not N) has an odd factor then we can represent it as a sum of a consecutive number
After this we have to only check whether we can represent (2N as
) or not
- if Yes then answer is false or 0
- if No then answer is true or 1
Below is the implementation of the above idea :
C++14
#include <bits/stdc++.h>
using namespace std;
long long int canBeSumofConsec( long long int n)
{
n = 2 * n;
return ((n & (n - 1)) != 0);
}
int main()
{
long long int n = 10;
cout<<canBeSumofConsec(n)<< "\n" ;
}
C
#include <stdio.h>
long long int canBeSumofConsec( long long int n)
{
n = 2 * n;
return ((n & (n - 1)) != 0);
}
int main()
{
long long int n = 10;
printf ( "%lld" , canBeSumofConsec(n));
}
Java
import java.util.*;
class GFG{
static int canBeSumofConsec( int n)
{
n = 2 * n;
return ((n & (n - 1 )) != 0 )? 1 : 0 ;
}
public static void main(String[] args)
{
int n = 10 ;
System.out.print(canBeSumofConsec(n)+ "\n" );
}
}
Python3
def canBeSumofConsec(n):
n = 2 * n;
if ((n & (n - 1 )) ! = 0 ):
return 1 ;
else :
return 0 ;
if __name__ = = '__main__' :
n = 10 ;
print (canBeSumofConsec(n));
C#
using System;
public class GFG {
static int canBeSumofConsec( int n)
{
n = 2 * n;
return ((n & (n - 1)) != 0) ? 1 : 0;
}
public static void Main(String[] args) {
int n = 10;
Console.Write(canBeSumofConsec(n) + "\n" );
}
}
Javascript
<script>
function canBeSumofConsec(n) {
n = 2 * n;
return ((n & (n - 1)) != 0) ? 1 : 0;
}
var n = 10;
document.write(canBeSumofConsec(n) + "\n" );
</script>
Time Complexity: O(1)
Auxiliary Space: O(1)
Reference:
http://www.cut-the-knot.org/arithmetic/UnpropertyOfPowersOf2.shtml
This article is contributed by Sahil Chhabra. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.
Source: https://www.geeksforgeeks.org/check-number-can-expressed-sum-consecutive-numbers/
0 Response to "Is It Possible to Write the Sum of Natural Numbers as a Continuous Funtion"
Post a Comment